Aperture (`pyoof.aperture`)¶

Introduction¶

The aperture sub-package contains related distributions/functions to the aperture distribution, \(\underline{E_\text{a}}(x, y)\). The aperture distribution is a two dimensional complex distribution, hence has an amplitude and a phase. The amplitude is represented by the blockage distribution, \(B(x, y)\), and the illumination function, \(E_\text{a}(x, y)\). The phase is given by the aperture phase distribution, \(\varphi(x, y)\) and the optical path difference (OPD) function, \(\delta(x,y;d_z)\). The collection of all distributions/functions for the aperture distribution is then,

\[\underline{E_\text{a}}(x, y) = B(x, y)\cdot E_\text{a}(x, y) \cdot \mathrm{e}^{\mathrm{i} \{\varphi(x, y) + \frac{2\pi}{\lambda}\delta(x,y;d_z)\}}.\]

Between them, the blockage distribution and OPD function are strictly dependent on the telescope geometry, which is the reason why they are gathered in the telgeometry sub-package.

Note

All mentioned Python functions are for a two dimensional analysis and they require as an input meshed values. They can also be used in one dimensional analysis by adding y=0 to each of the Python functions. Although their analysis in the pyoof package is strictly two dimensional.

To generate meshed values simply use the meshgrid routine.

>>> import numpy as np
>>> x = np.linspace(-50, 50, 1e3)
>>> xx, yy = np.meshgrid(x, x)  # values in a grid

Note

A Jupyter notebook tutorial for the aperture sub-package is provided in the aperture.ipynb on the GitHub repository.

Lastly there is another distribution left which is the (field) radiation pattern, \(F(u, v)\), which is the direct Fourier Transform (in two dimensions) of the aperture distribution (both of them being complex numbers).

\[F(u, v) = \mathcal{F}\left[\underline{E_\text{a}}(x, y)\right]\]

The (field) radiation pattern is the most extensive function in this sub-package. The standard Python package fft2 is used to compute the FFT in two dimensions.

Using `aperture`¶

Using the aperture package is really simple, for example the illumination function, \(E_\text{a}(x, y)\),

import numpy as np
import matplotlib.pyplot as plt
from pyoof import aperture

pr = 50  # primary relfector m
x = np.linspace(-pr, pr, 1e3)
xx, yy = np.meshgrid(x, x)

I_coeff = [1, -14, 0, 0]  # [amp, c_dB, x0, y0]

Ea = aperture.illum_pedestal(xx, yy, I_coeff, pr)
Ea[xx ** 2 + yy ** 2 > pr ** 2] = 0  # circle shape

fig, ax = plt.subplots()
ax.imshow(Ea, extent=[-pr, pr] * 2, cmap='viridis')
ax.set_xlabel('$x$ m')
ax.set_ylabel('$y$ m')
ax.set_title('Illumination function')

(png, svg, pdf)

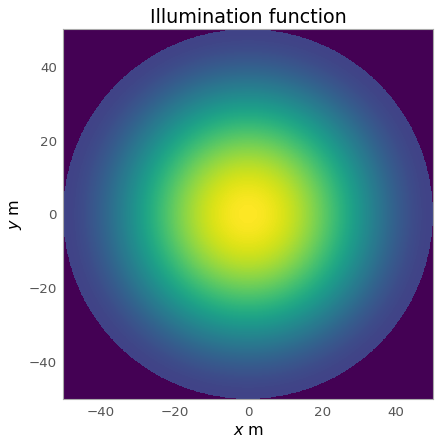
The aperture only uses standard Python libraries, but what needs special consideration are the Python functions with the parameter K_coeff, coming up.

Wavefront (aberration) distribution \(W(x, y)\)¶

The wavefront (aberration) distribution, \(W(x, y)\), is strictly related to the aperture phase distribution (see Jupyter notebook, zernike.ipynb on GitHub), and it is the basis of the nonlinear least squares minimization done by the pyoof package.

Note

The Zernike circle coefficients, given by K_coeff are the basic structure for the aperture phase distribution. It is important to note that for an order \(n\) of the polynomial there are \((n+1)(n+2)/2\) total number of polynomials. See zernike.

One basic example is to plot \(W(x, y)\) with a random set of Zernike circle polynomial coefficients.

import numpy as np
import matplotlib.pyplot as plt
from pyoof import aperture, cart2pol

pr = 50  # primary relfector m
n = 10  # order polynomial
N_K_coeff = (n + 1) * (n + 2) // 2  # max polynomial number
K_coeff = np.random.normal(0., .1, N_K_coeff)

# Generating the mesh
x = np.linspace(-pr, pr, 1e3)
xx, yy = np.meshgrid(x, x)
r, t = cart2pol(xx, yy)
r_norm = r / pr  # polynomials uner unitary circle

W = aperture.wavefront(rho=r_norm, theta=t, K_coeff=K_coeff)
W[xx ** 2 + yy ** 2 > pr ** 2] = 0

fig, ax = plt.subplots()
ax.contour(xx, yy, W, colors='k', alpha=0.3)
ax.imshow(W, extent=[-pr, pr] * 2, origin='lower', cmap='viridis')

ax.set_title('Wavefront (aberration) distribution')
ax.set_ylabel('$y$ m')
ax.set_xlabel('$x$ m')

(png, svg, pdf)

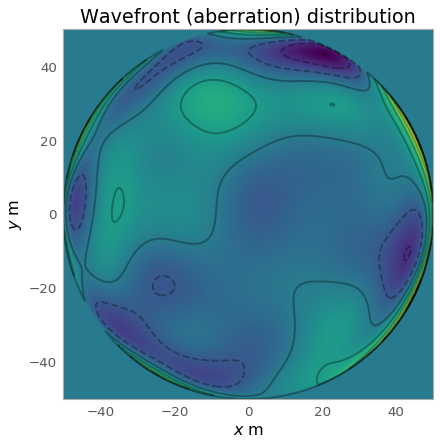
Aperture phase distribution \(\varphi(x, y)\)¶

The calculation of the aperture phase distribution, phase, follows the same guidelines as the wavefront (aberration) distribution, wavefront. In general, the problem will only focus on the aperture phase distribution, and not on the wavefront (aberration) distribution. To compute the phase simply,

import numpy as np
import matplotlib.pyplot as plt
from pyoof import aperture

pr = 50  # primary relfector m
n = 5  # order polynomial
N_K_coeff = (n + 1) * (n + 2) // 2  # max polynomial number
K_coeff = np.random.normal(0., .1, N_K_coeff)

x, y, phi_notilt = aperture.phase(K_coeff=K_coeff, notilt=True, pr=pr)
phi_tilt = aperture.phase(K_coeff=K_coeff, notilt=False, pr=pr)[2]

levels = np.linspace(-2, 2, 9)

fig, ax = plt.subplots(ncols=2)

for data, i in zip([phi_notilt, phi_tilt], range(2)):
    ax[i].imshow(
        data, extent=[-pr, pr] * 2, origin='lower', cmap='viridis'
        )
    ax[i].contour(x, y, data, levels=levels, alpha=0.3, colors='k')
    ax[i].set_xlabel('$x$ m')
    ax[i].set_ylabel('$y$ m')

ax[0].set_title('$\\varphi(x, y)$ no-tilt')
ax[1].set_title('$\\varphi(x, y)$')

fig.tight_layout()

(png, svg, pdf)

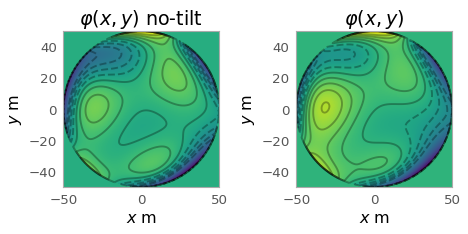
To study the aberration in the aperture phase distribution, first it is necessary to remove some telescope effects. These are the tilt terms and are related to the telescope’s pointing and become irrelevant. The tilt terms also represent the average slope in the \(x\) and \(y\) directions. In the Zernike circle polynomials the tilt terms are \(K^1_1\) and \(K^{-1}_1\). To erase their dependence they are set to zero.

Aperture distribution \(\underline{E_\text{a}}(x, y)\)¶

To compute the aperture distribution, two extra functions from the telgeometry package are required. Assuming the reader knows them, it is easy to compute \(\underline{E_\text{a}}(x, y)\),

import numpy as np
import matplotlib.pyplot as plt
from pyoof import aperture, telgeometry

pr = 50  # primary relfector m
n = 5  # order polynomial
N_K_coeff = (n + 1) * (n + 2) // 2  # max polynomial number
K_coeff = np.random.normal(0., .1, N_K_coeff)

taper = np.random.randint(-20, -8)  # random illumination taper
I_coeff = [1, taper, 0, 0]

# Generating the mesh
x = np.linspace(-pr, pr, 1e3)
xx, yy = np.meshgrid(x, x)

# For these functions see telgeometry sub-package
telgeo = [telgeometry.block_effelsberg, telgeometry.opd_effelsberg, pr]

Ea = []
for d_z in [-.022, 0, .022]:

    Ea.append(
        aperture.aperture(
            x=xx, y=yy,
            K_coeff=K_coeff,
            I_coeff=I_coeff,
            d_z=d_z,  # radial offset
            wavel=0.009,  # observation wavelength
            illum_func=aperture.illum_pedestal,
            telgeo=telgeo  # see telgeometry sub-package
            )
        )

extent = [-pr, pr] * 2

fig, axes = plt.subplots(ncols=3, nrows=2)
ax = axes.flat

for i in range(3):
    ax[i].imshow(Ea[i].real, cmap='viridis', origin='lower', extent=extent)
    ax[i + 3].imshow(
        Ea[i].imag, cmap='viridis', origin='lower', extent=extent
        )
    ax[i].contour(xx, yy, Ea[i].real, cmap='viridis')
    ax[i + 3].contour(xx, yy, Ea[i].imag, cmap='viridis')

ax[0].set_title('Aperture real $d_z^-$')
ax[1].set_title('Aperture real $d_z$')
ax[2].set_title('Aperture real $d_z^+$')
ax[3].set_title('Aperture imag $d_z^-$')
ax[4].set_title('Aperture imag $d_z$')
ax[5].set_title('Aperture imag $d_z^+$')

# Turn off tick labels
for _ax in ax:
    _ax.set_yticklabels([])
    _ax.set_xticklabels([])

fig.tight_layout()

(png, svg, pdf)

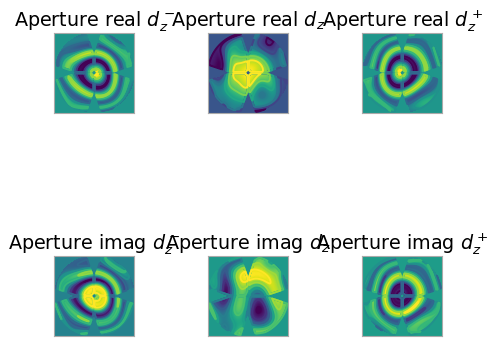
As mentioned before the aperture distribution is complex, which also depends on the radial offset added to defocus the telescope. Depending on that its shape in the real and imaginary parts will change. In general, the aperture distribution will not be used for the OOF holography study, only the power pattern and phase error will be used for visual inspection.

In contrast the (field) radiation pattern, has the same inputs, except for the fft2 routine, which requires two more important parameters. These are resolution and box_factor. Hence, it is simply executed by,

import numpy as np
import matplotlib.pyplot as plt
from pyoof import aperture, telgeometry

pr = 50  # primary relfector m
n = 5  # order polynomial
N_K_coeff = (n + 1) * (n + 2) // 2  # max polynomial number
K_coeff = np.random.normal(0., .1, N_K_coeff)

taper = np.random.randint(-20, -8)  # random illumination taper
I_coeff = [1, taper, 0, 0]

telgeo = [telgeometry.block_effelsberg, telgeometry.opd_effelsberg, pr]

F = aperture.radiation_pattern(
    K_coeff=K_coeff,
    I_coeff=I_coeff,
    d_z=0,  # in the cm order
    wavel=0.009,  # observation wavelength
    illum_func=aperture.illum_pedestal,
    telgeo=telgeo,
    resolution=2 ** 8,
    box_factor=5 * pr
    )

Reference/API¶

pyoof.aperture Package¶

This sub-package contains all necessary functions to compute the aperture distribution and the (field) radiation pattern, and is ready to be used by the least squares minimization.

Functions¶

`aperture`(x, y, K_coeff, I_coeff, d_z, wavel, ...)	Aperture distribution, \(\underline{E_\mathrm{a}}(x, y)\).
`e_rs`(phase)	Computes the random-surface-error efficiency, \(\varepsilon_\mathrm{rs}\), using the Ruze’s equation.
`illum_gauss`(x, y, I_coeff, pr)	Illumination function, \(E_\mathrm{a}(x, y)\), Gaussian, sometimes called apodization, taper or window.
`illum_pedestal`(x, y, I_coeff, pr[, q])	Illumination function, \(E_\mathrm{a}(x, y)\), parabolic taper on a pedestal, sometimes called apodization, taper or window.
`phase`(K_coeff, notilt, pr[, resolution])	Aperture phase distribution (or phase error), \(\varphi(x, y)\), for an specific telescope primary reflector.
`radiation_pattern`(K_coeff, I_coeff, d_z, ...)	Spectrum or (field) radiation pattern, \(F(u, v)\), it is the FFT2 computation of the aperture distribution, \(\underline{E_\mathrm{a}} (x, y)\), in a rectangular grid.
`wavefront`(rho, theta, K_coeff)	Computes the wavefront (aberration) distribution, \(W(x, y)\).

Aperture (`pyoof.aperture`)¶

Introduction¶

Using `aperture`¶

Wavefront (aberration) distribution \(W(x, y)\)¶

Aperture phase distribution \(\varphi(x, y)\)¶

Aperture distribution \(\underline{E_\text{a}}(x, y)\)¶

See Also¶

Reference/API¶

pyoof.aperture Package¶

Functions¶

Page Contents

Navigation

Aperture (pyoof.aperture)¶

Introduction¶

Using aperture¶

Wavefront (aberration) distribution \(W(x, y)\)¶

Aperture phase distribution \(\varphi(x, y)\)¶

Aperture distribution \(\underline{E_\text{a}}(x, y)\)¶

See Also¶

Reference/API¶

pyoof.aperture Package¶

Functions¶

Aperture (`pyoof.aperture`)¶

Using `aperture`¶